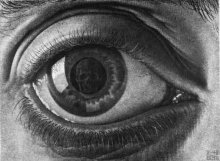
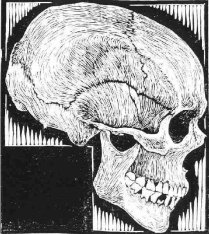
Σαν σήμερα πριν από 119 χρόνια γεννήθηκε ο εικαστικός καλλιτέχνης M. C. Escher (17/6/1898–27/3/1972), ο άνθρωπος που αφιέρωσε τη ζωή του στην απεικόνιση του αδύνατου. Γιατί; Επειδή μπορούσε.—του Γιώργου Θεοχάρη—
Ελάχιστα βιογραφικά στοιχεία
Γεννήθηκε στην Ολλανδία. Ο πατέρας του ήταν πολιτικός μηχανικός. Ως παιδί, ήταν φιλάσθενος, πράγμα που εξηγεί μερικώς την ελλιπή του εκπαίδευση. Στο σχολείο τα πήγαινε παντού χάλια – εκτός από το σχέδιο. Προσπάθησε να σπουδάσει αρχιτεκτονική, αλλά δεν τα κατάφερε, κι έτσι στράφηκε στη χαρακτική (λιθογραφία, ξυλογραφία, χαλκογραφία). Το 1922 ταξίδεψε στην Ιταλία και την Ισπανία. Αυτό έμελλε να είναι το ταξίδι που άλλαξε τη ζωή του. Στη Γρανάδα εντυπωσιάστηκε από την Αλάμπρα, το μαυριτανικό κάστρο του 14
ου αιώνα. Τα περίτεχνα διακοσμητικά σχέδια με τα επαναλαμβανόμενα μοτίβα που είδε εκεί του κίνησαν το ενδιαφέρον για τις γεωμετρικές συμμετρίες, μια επιρροή φανερή σε όλο του το έργο. Στην Ιταλία γνώρισε την Jetta Umiker, με την οποία παντρεύτηκε το 1924. Απέκτησαν τρεις γιους. Έμειναν στη Ρώμη μέχρι το 1935, οπότε και έφυγαν μην αντέχοντας την Ιταλία του Mussolini. Ο Escher δεν ενδιαφερόταν για την πολιτική, αλλά απεχθανόταν τον φανατισμό, και προφανώς ο ιταλικός φασισμός τού έπεσε βαρύς. Με ενδιάμεσους σταθμούς την Ελβετία και το Βέλγιο, η οικογένεια κατέληξε το 1942 στην Ολλανδία, όπου και στέριωσε. Εκεί ο Escher φιλοτέχνησε το μεγαλύτερο μέρος του έργου για το οποίο έγινε διάσημος.
Συμβολή στην Ποιητική των ΜαθηματικώνΔεν υπάρχει περίπτωση να γίνει λόγος για «Τέχνη και Μαθηματικά» χωρίς αναφορά στον Escher. Αυτό που κυρίως χαρακτηρίζει το έργο του είναι η απεικόνιση του αδύνατου: γραφικές παραστάσεις ανθρώπων, ζώων, αντικειμένων, οι οποίες δημιουργούν την ψευδαίσθηση του απείρου (μοτίβα που δεν τελειώνουν ποτέ και πουθενά, παράδοξες αρχιτεκτονικές δομές, οφθαλμαπάτες). Για να απεικονίσει το αδύνατο, ο Escher χρησιμοποίησε ποιητικά τα μαθηματικά (προβολική γεωμετρία, τοπολογία, μη ευκλείδεια γεωμετρία).
Κρίνοντας από τις ακαδημαϊκές του επιδόσεις, ο Escher λογικά δεν έμαθε μαθηματικά στο σχολείο. Εντούτοις, είχε τα μαθηματικά μέσα του: τα διαισθανόταν, τα «έβλεπε»∙ τα ζούσε. Οι διακοσμήσεις που είδε στην Αλάμπρα τον ενέπνευσαν να χρησιμοποιήσει γεωμετρικά πλέγματα ως βάση των σχεδίων του, τα οποία επικάλυπτε με σχέδια ζώων (πουλιών, λιονταριών κ.λπ.). Έτσι άρχισαν όλα.
(...)Οι μαθηματικοί εκτιμούν ιδιαίτερα τα ψηφιδωτά του με τα επαναλαμβανόμενα μοτίβα, τη χρήση των πολυέδρων και τις γεωμετρικές παραμορφώσεις του. Δείτε, λόγου χάριν, τη
Βαρύτητα, όπου πολύχρωμες χελώνες βγάζουν τα κεφάλια τους μέσα από ένα ψηφιδωτό δωδεκάεδρο.
Στη
Μεταμόρφωση 1 (1937), μετέτρεψε ένα κυρτό πολύγωνο σε κανονικό σχέδιο στο επίπεδο ώστε να σχηματίσει μία ανθρώπινη φιγούρα. Το έργο αυτό σηματοδοτεί την αλλαγή του ενδιαφέροντος του από τα φυσικά τοπία στην κανονική διαίρεση του επιπέδου. Τα μαθηματικά είχαν πλέον μπει για τα καλά στο έργο του.
Metamorphosis I Το 1958 ο Escher εξέδωσε ένα βιβλίο, με τίτλο
“Regular Division of the Plane” («
Κανονική Διαίρεση του Επιπέδου»), στο οποίο είχε συγκεντρώσει εκείνες τις ξυλογραφίες στο επίπεδο τις οποίες θεωρούσε αντιπροσωπευτικές για την επιρροή των μαθηματικών στο έργο του. Εκεί σημείωνε: «Οι μαθηματικοί έχουν ανοίξει έναν δρόμο προς ένα ανεξάντλητο πεδίο».
Η προσήλωσή του στην έννοια της κανονικής διαίρεσης του επιπέδου φαίνεται ήδη από τα ιταλικά τοπία της πρώτης περιόδου του. Κάτι δεν του άρεσε εξαρχής με την
επιπεδοσύνη των δύο διαστάσεων. Είχε καταφανώς ένα θέμα με τις δύο διαστάσεις. Μπορεί να δούλευε (εκ των πραγμάτων) στο επίπεδο, αλλά ένιωθε ότι η έλλειψη βάθους τον περιόριζε. «Θέλω», έλεγε, «ν’ αναγκάσω τα πράγματα να βγουν από το επίπεδο». (Δείτε τι εννοούσε, για παράδειγμα, στα
Χέρια που Σχεδιάζουν.)
Ακόμα και πριν μελετήσει μαθηματικά, έκανε χρήση προβολής του υπερβολικού επιπέδου σε δεδομένο δισδιάστατο επίπεδο. Σταδιακά, άρχισε να ενσωματώνει στα έργα του τρισδιάστατα αντικείμενα όπως σφαίρες, κώνους, κύβους, δακτύλιους, έλικες. (Για ένα χαρακτηριστικό παράδειγμα συνδυασμού δισδιάστατων και τρισδιάστατων εικόνων δείτε τα
Ερπετά.)
Μελέτησε επίσης τοπολογία (= η μελέτη των συνόλων στα οποία μπορεί να οριστεί μια έννοια «κλειστότητας» έτσι ώστε να διακρίνεται η συνέχεια για οποιαδήποτε συνάρτηση που ορίζεται σε αυτά). Συνέχιζε να μαθαίνει μαθηματικά, συζητώντας με τον Βρετανό μαθηματικό Roger Penrose. Δείγματα των νέων θεωρητικών κατακτήσεων αντανακλώνται σε έργα με ακανόνιστη προοπτική (βλ.
Λωρίδα του Μέμπιους), όπως τα
Καταρράκτης και
Πάνω και Κάτω.
Καταρράχτης
Πάνω και ΚάτωΕν κατακλείδι, ο Escher, εκτός από μεγαλοφυής εικαστικός, υπήρξε ερασιτέχνης (με την παλιά έννοια) μαθηματικός. Αλλιώς: ο Escher οφείλει την περίοπτη θέση του στην Ιστορία της Τέχνης (και) στα μαθηματικά.
Ο Escher πρόσθεσε διαστάσεις στο επίπεδο με έναν τρόπο που δεν έχει προηγούμενο. Σχεδίασε αυτό που δεν υπάρχει∙ άγγιξε το αδύνατο – αλλά αυτό το είχαν κάνει και άλλοι πριν από αυτόν. Όχι όμως με τον δικό του, μοναδικό τρόπο. Εκ των υστέρων, μπορεί κανείς να δει ότι ο Escher δεν θα μπορούσε να υπάρξει παρά μόνο στον 20ό αιώνα. Το έργο του χαρακτηρίζει όσο λίγων άλλων αυτή την περίπλοκη (και γι’ αυτό άκρως ενδιαφέρουσα) περίοδο της ανθρώπινης ιστορίας.
Είναι εφικτό το αδύνατο; Όχι, αλλά δεν δικαιούσαι να έχεις λόγο αν δεν τολμήσεις να το επιτύχεις. Με άλλα λόγια, είναι εφικτό να
τολμήσεις το αδύνατο. Αυτό ακριβώς έκανε ο M. C. Escher.
Ο Μπόρλγκρουμ πέθανε εφτά μήνες πριν το εμβληματικό του έργο παραδοθεί. Την ολοκλήρωση ανέλαβε ο γιος του, Λίνκολν. Το δημιούργημα του Μπόρλγκρουμ εντυπωσιάζει ακόμα κι σήμερα τους εκατομμύρια τουρίστες που το επισκέπτονται κάθε χρόνο και αποτελεί σημείο αναφοράς για τους Αμερικανούς....
